Last Updated on September 29, 2023
Multithreaded matrix multiplication in numpy is faster than single-threaded matrix multiplication.
The speed-up factor can range from slightly above 1.2x to nearly 3x, depending on the size of the matrices that are being multiplied. It is possible that multiplying smaller matrices, such as 100×100 or smaller may result in worse performance when using threads.
In this tutorial, you will discover how to benchmark numpy multithreaded matrix multiplication.
Let’s get started.
Numpy Matrix Multiplication is Multithreaded
NumPy is an array library in Python.
NumPy supports many linear algebra functions with vectors and arrays by calling into efficient third-party libraries such as BLAS and LAPACK.
BLAS and LAPACK are specifications for efficient vector, matrix, and linear algebra operations that are implemented using third-party libraries, such as MKL and OpenBLAS. Some operations in these libraries, such as matrix multiplication, are multithreaded.
You can learn more about NumPy and BLAS in the tutorial:
Run loops using all CPUs, download your FREE book to learn how.
How Does Multithreaded Matrix Multiplication Compare
Matrix multiplication is a central task in linear algebra.
Given that numpy supports multithreaded matrix multiplication via an installed BLAS library, we may be curious about the sped benefits it offers.
For example, how much more efficient is multithreaded matrix multiplication compared to single-threaded matrix multiplication, at least with modestly sized matrices?
Is matrix multiplication always multithreaded or are threads only used with matrices above a certain size?
We can explore these questions by benchmarking matrix multiplication with differently sized matrices firstly without threads, then with threads, then comparing the results.
Benchmark Single Threaded Matrix Multiplication
We can benchmark how long it takes to multiply modestly sized matrices using a single thread.
This can be achieved by configuring the installed BLAS library to use a single thread. We can implement this by setting an environment variable prior to loading the numpy library, either as an environment variable or within our code via the os.environ() function.
For example, the following will configure BLAS/LAPACK to use a single thread on most systems:
|
1 2 3 |
... from os import environ environ['OMP_NUM_THREADS'] = '1' |
You can learn more about configuring the number of threads used by BLAS and LAPACK in the tutorial:
We can define a task that benchmarks matrix multiplication for a matrix of a given size.
The task will first create two matrices of a given size filled with random floating point values. These are then multiplied together using the dot() method on the numpy array object. The start time is recorded before the operation and the end time at the end of the operation so that the duration can be calculated.
This task is then repeated a fixed number of times, such as 30, then the average result is reported. We repeat the experiments many times and report the average to overcome randomness in the experiment.
The task() function below implements this, taking a matrix size as an argument and returning the average time taken to multiply two square matrices of the given size.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# multiply two matrices and report how long it takes def task(n, repeats=30): results = list() for _ in range(repeats): # record start time start = time() # create an array of random values data1 = rand(n, n) data2 = rand(n, n) # matrix multiplication result = data1.dot(data2) # calculate the duration in seconds duration = time() - start # store result results.append(duration) # return the average return sum(results) / repeats |
We can then perform this task to benchmark matrices of different sizes.
In this case, we will benchmark 10 matrix sizes from 100×100 to 1000×1000 and report the time of each.
We will focus on these smaller-sized matrices because we want to know if multiplying small matrices is multithreaded and because the small sizes mean that the experiment will be completed in a reasonable time on all systems.
|
1 2 3 4 5 6 7 |
... # report time of matrix multiplication for each matrix size for size in range(100,1100,100): # perform task and record time result = task(size) # report result print(f'{size} took {result:.6f} seconds') |
Tying this together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# benchmark of single threaded matrix multiplication from os import environ environ['OMP_NUM_THREADS'] = '1' from time import time from numpy.random import rand # multiply two matrices and report how long it takes def task(n, repeats=30): results = list() for _ in range(repeats): # record start time start = time() # create an array of random values data1 = rand(n, n) data2 = rand(n, n) # matrix multiplication result = data1.dot(data2) # calculate the duration in seconds duration = time() - start # store result results.append(duration) # return the average return sum(results) / repeats # report time of matrix multiplication for each matrix size for size in range(100,1100,100): # perform task and record time result = task(size) # report result print(f'{size} took {result:.6f} seconds') |
Running the example reports the average time taken in seconds to multiply matrices together of different sizes.
We can see that all sizes are completed in under one second on average when using a single thread.
|
1 2 3 4 5 6 7 8 9 10 |
100 took 0.000162 seconds 200 took 0.000790 seconds 300 took 0.002046 seconds 400 took 0.004076 seconds 500 took 0.007471 seconds 600 took 0.012077 seconds 700 took 0.017839 seconds 800 took 0.025071 seconds 900 took 0.034799 seconds 1000 took 0.045507 seconds |
Next, let’s complete the same experiment using multiple threads.
Free Concurrent NumPy Course
Get FREE access to my 7-day email course on concurrent NumPy.
Discover how to configure the number of BLAS threads, how to execute NumPy tasks faster with thread pools, and how to share arrays super fast.
Benchmark Multithreaded Matrix Multiplication
We can benchmark matrix multiplication using multiple threads.
This can be achieved by configuring the number of BLAS threads to be equal to the number of physical CPUs in the system.
I have 4 physical CPUs in my system therefore, I will configure BLAS to use 4 CPUs. Update the configuration to match the number of physical CPUs in your system.
|
1 2 3 |
... from os import environ environ['OMP_NUM_THREADS'] = '4' |
We could just remove these two lines and use multithreaded BLAS with the default number of CPUs. I prefer not to do this as I often see better performance when configuring the number of CPUs manually on my system.
You can learn more about configuring the number of CPUs used by numpy and BLAS in the tutorial:
The complete example with this change is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# benchmark of multithreaded matrix multiplication from os import environ environ['OMP_NUM_THREADS'] = '4' from time import time from numpy.random import rand # multiply two matrices and report how long it takes def task(n, repeats=30): results = list() for _ in range(repeats): # record start time start = time() # create an array of random values data1 = rand(n, n) data2 = rand(n, n) # matrix multiplication result = data1.dot(data2) # calculate the duration in seconds duration = time() - start # store result results.append(duration) # return the average return sum(results) / repeats # report time of matrix multiplication for each matrix size for size in range(100,1100,100): # perform task and record time result = task(size) # report result print(f'{size} took {result:.6f} seconds') |
Running the example reports the average time taken in seconds to multiple matrices of different sizes, this time using 4 worker threads.
Again, each matrix size is less than one second.
|
1 2 3 4 5 6 7 8 9 10 |
100 took 0.000186 seconds 200 took 0.000644 seconds 300 took 0.001593 seconds 400 took 0.002850 seconds 500 took 0.005116 seconds 600 took 0.007525 seconds 700 took 0.012027 seconds 800 took 0.013756 seconds 900 took 0.018327 seconds 1000 took 0.023593 seconds |
Next, let’s compare the results of single vs multithreaded matrix multiplication in numpy using BLAS.
Overwhelmed by the python concurrency APIs?
Find relief, download my FREE Python Concurrency Mind Maps
Comparison of Multithreaded Matrix Multiplication Results
We can now compare the results of single vs multithreaded matrix multiplication with different modestly sized matrices.
The table below summarizes the average time taken to multiply each matrix size using one and four threads.
|
1 2 3 4 5 6 7 8 9 10 11 |
Matrix Size Time 1 Thread Time 4 Threads 100 0.000162 0.000186 200 0.00079 0.000644 300 0.002046 0.001593 400 0.004076 0.00285 500 0.007471 0.005116 600 0.012077 0.007525 700 0.017839 0.012027 800 0.025071 0.013756 900 0.034799 0.018327 1000 0.045507 0.023593 |
The plot below summarizes the data, comparing the average time taken with both one and four threads.
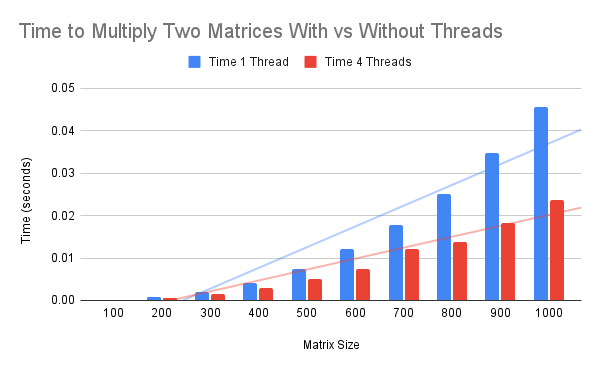
We can see that in all but the first matrix size, the multithreaded example was faster than the single-threaded example.
The results suggest that multithreading may always be used for matrix multiplication if enabled. At least for matrices of 100×100 in size and above.
The slightly slower average time taken for a 100×100 matrix suggests that multithreading hurts performance in this case, rather than helps it.
We can compare the results directly.
Firstly, we can subtract the multithreaded time from the single-threaded time to give the average difference in time.
Secondly, we can divide the multithreaded time by the single-threaded time to give a speed-up factor.
The table below summarizes the results.
|
1 2 3 4 5 6 7 8 9 10 11 |
Matrix Size Time 1 Thread Time 4 Threads Difference Speed-up 100 0.000162 0.000186 -0.000024 0.8709677419 200 0.00079 0.000644 0.000146 1.226708075 300 0.002046 0.001593 0.000453 1.284369115 400 0.004076 0.00285 0.001226 1.430175439 500 0.007471 0.005116 0.002355 1.460320563 600 0.012077 0.007525 0.004552 1.604916944 700 0.017839 0.012027 0.005812 1.48324603 800 0.025071 0.013756 0.011315 1.82255016 900 0.034799 0.018327 0.016472 1.898783216 1000 0.045507 0.023593 0.021914 1.928834824 |
The plot below summarizes the speed-up of the multithreaded version over the single-threaded version for each matrix size.
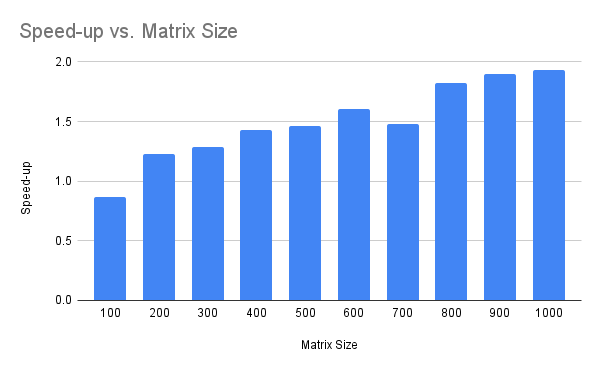
The plot shows that the smaller matrices approach a 1.5x speed-up whereas the larger matrices approach a 2x speed-up.
We can see a clear trend of an increasing speed-up factor with matrix size.
I suspect that this trend will continue. That is, a larger speed-up factor will be observed as the matrix size is increased. At least to a point where matrices are too large to fit in a specific CPU cache or main memory.
In fact, we can extend the experiment to larger matrices and observe the trend.
The table below summarizes results from multiplying 2,000×2,000 matrices up to 10,000×10,000 matrices, stepped up in increments of 2,000.
|
1 2 3 4 5 6 |
Matrix Size Time 1 Thread Time 4 Threads Difference Speed-up 2000 0.294893 0.121557 0.173336 2.425964774 4000 2.21648 0.804028 1.412452 2.756719915 6000 7.24536 2.548271 4.697089 2.843245479 8000 16.703071 5.912314 10.790757 2.825132596 10000 32.542176 12.38683 20.155346 2.62715933 |
The plot below summarizes the results.
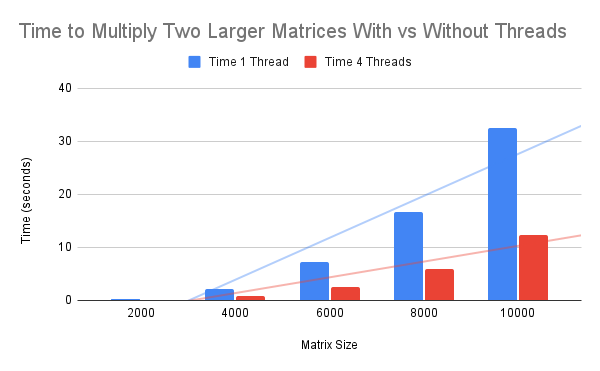
We can see from the table that in all cases tested, the multithreaded version is more than 2x faster than the single-threaded version.
The trend does increase with matrix size, although it is perhaps leveling out or even reversing as we reach 10,000×10,000 matrices.
Further Reading
This section provides additional resources that you may find helpful.
Books
- Concurrent NumPy in Python, Jason Brownlee (my book!)
Guides
- Concurrent NumPy 7-Day Course
- Which NumPy Functions Are Multithreaded
- Numpy Multithreaded Matrix Multiplication (up to 5x faster)
- NumPy vs the Global Interpreter Lock (GIL)
- ThreadPoolExecutor Fill NumPy Array (3x faster)
- Fastest Way To Share NumPy Array Between Processes
Documentation
- Parallel Programming with numpy and scipy, SciPi Cookbook, 2015
- Parallel Programming with numpy and scipy (older archived version)
- Parallel Random Number Generation, NumPy API
NumPy APIs
Concurrency APIs
- threading — Thread-based parallelism
- multiprocessing — Process-based parallelism
- concurrent.futures — Launching parallel tasks
Takeaways
You now know how to benchmark numpy multithreaded matrix multiplication.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.



Leave a Reply